Beispiel 1: Die kurzfristigen Kostenfunktionen verlaufen oberhalb der langfristigen und tangieren diese in einem Punkt.

Die (neoklassische) Produktionsfunktion einer Unternehmung sei

$$ x = K^{1/6}L^{2/6} \tag{1} $$

Wenn die Faktorpreise $w=12$ und $r=64$ sind, bestimmt man den Expansionspfad zu $K=L$, d.h. die Unternehmung produziert kostenminimal mit einer Kapitalintensität von eins. Die langfristigen Kosten sind

$$ C = 12L + 6K = 18K = 18x^2 \tag{2} $$

Jetzt sei $K$ kurzfristig konstant gleich eins gemessen in "Produktionsstätten". D.h. auf kurze Sicht produziert die betrachtete Unternehmung mit einer Produktionsstätte, die Fixkosten in Höhe von 6 verursacht, so dass die kurzfristigen Kosten gegeben sind durch

$$ C = 6 + 12L = 6 + 12x^3 \tag{3} $$

Die beiden Kostenfunktionen haben (wie man durch Gleichsetzen von (2) und (3) nachrechnet) nur einen Punkt gemeinsam: $x = 1$. Nur bei einer Produktionsmenge von eins ist die Kapitalintensität auch kurzfristig optimal. Ansonsten verläuft die kurzfristige Kostenfunktion immer oberhalb der langfristigen.

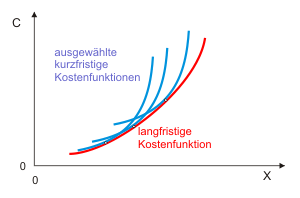
Die langfristige Kostenfunktion "umhüllt" alle kurzfristigen Kostenfunktionen "von unten" (s. Skizze). Dazu sei betrachtet, dass die Menge $x = 8$ hergestellt wird. Die optimale Betriebsgröße wäre dann bei $K = 64$ Produktionsstätten gegeben. Die kurzfristige Kostenfunktion wäre jetzt

$$ C = 6 \cdot 64 + 12L = 384 + 1,5x^3 \tag{4} $$

denn wegen $K=L$ ist $ x = 64^{1/6}L^{2/6} = 2L^{1/3}$

Also muss die Produktion von $x = 8$ kurz- wie langfristig gleich teuer, die Produktion abweichender Mengen jedoch langfristig günstiger sein als kurzfristig:

Menge	kurzfr. Kosten	langfr. Kosten
Q=7	898,5	882,0
Q=8	1152,0	1152,0
Q=9	1477,5	1458,0

 

Beispiel 2: Langfristiges Gleichgewicht, optimale Zahl der Unternehmen

 

Eine repräsentative Unternehmung besitze die ertragsgesetzliche langfristige Kostenfunktion

$$ C = 0,1x^3 - 2x^2 + 15x \tag{5} $$

Momentan sei zu beobachten, dass auf dem Markt 1.000 Stück zu einem Preis von 5 gehandelt werden. Handelt es sich um ein langfristiges Gleichgewicht? Wenn ja, wie viele Unternehmen sind am Markt?

Lösung:

Die langfristigen Durchschnittskosten sind

$$ DK = \cfrac{C}{x} = 0,1x^2 - 2x + 15 \tag{6} $$

Das Minimum der langfristigen Durchschnittskosten (Betriebsoptimum) liegt bei $x=10$. Bei dieser Produktionsmenge stimmen die Stückkosten mit dem Preis in Höhe von 5 überein, wie man durch Einsetzen in (6) nachrechnet. Die Unternehmen können demnach nur kostendeckend anbieten, wenn sie im Betriebsoptimum produzieren. Da dies eine Produktion von 10 Stück im Unternehmen erfordert, befinden sich 100 Unternehmen am Markt.

Würde der Preis auf 10 ansteigen, hätte jedes einzelne Unternehmen im Markt die Absicht, 11,94 Stück anzubieten, da diese Menge nach der Preis-Grenzkosten-Regel den Gewinn maximieren würde. Die Stückkosten betrügen dann allerdings nur 5,38. Die Gewinne würde neue Unternehmen in den Markt locken, das steigende Angebot den Preis drücken. Langfristig würde der Preis wieder auf 5 fallen, und die Unternehmen würden wieder im Betriebsoptimum produzieren.